Para poder explicar el dicho popular: Monte arriba, monte abajo… apunta bajo, necesitamos asentar una serie de conocimientos, que como cazador o tirador todos tenemos, aunque a veces no sepamos que los sabemos.
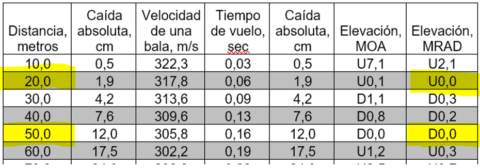
Usemos como ejemplo el disparo de un proyectil del calibre .22 con las características indicadas en la siguiente tabla.
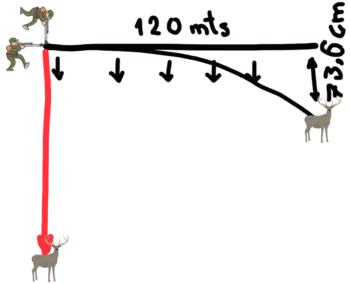
El disparo lo realizaremos horizontalmente a la superficie terrestre y subidos en una montaña.
Esto nos permitirá observar la caída del proyectil motivada por la fuerza de la gravedad, que lo atraerá hacia el centro del planeta.
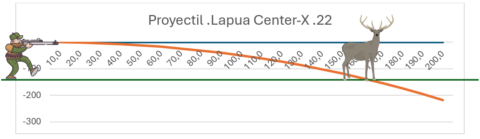
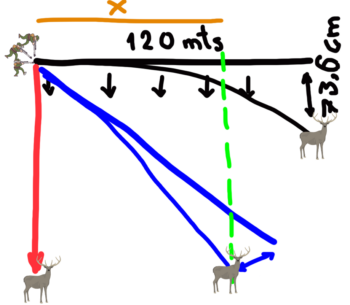
Calculamos dicha caída con una aplicación balística y ponemos los resultados en un gráfico que superpondremos a nuestro tirador subido en la montaña.
Ahora que ya visualizamos la parábola que describe el proyectil al salir por la boca del arma del tirador, podemos quitarlo de nuestra gráfica para poder ver más claro lo que pretendo explicar.
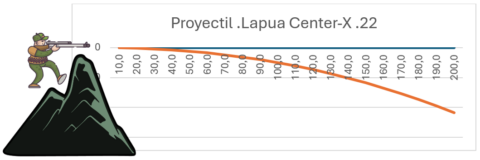
Teniendo en cuenta que en el gráfico se muestran los valores según los siguientes ejes:
• En el eje X representamos la distancia que recorre el proyectil en metros.
• En el eje Y representamos la caída de este según se aleja de la boca del cañón del arma.
Si el tirador estuviera sobre una superficie plana, en lugar de en el borde de una montaña, el proyectil se incrustaría en el suelo a antes de los 170 metros de su vuelo.
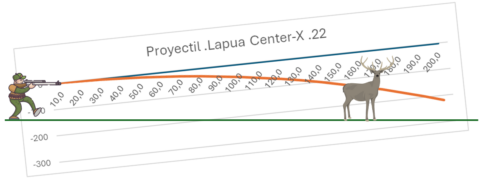
Así que, si pretendemos disparar a un objetivo y no queremos darle en la parte de debajo de las pezuñas o pies, ¿Qué tendremos que hacer?
Tendremos que elevar el tiro para hacer coincidir el punto de impacto con el mencionado objetivo.
Claro que… si el objetivo se acerca o se aleja, para apuntar, este pobre hombre lo va a tener muy complicado… excepto si dispone de una torreta balística que le permita “subir” o “bajar” la cruceta de su visor el número de MRAD (mili radianes) o MOAS (Minute Of Angle, en inglés, o minuto de ángulo en español) que le indique la tabla balística calculada para su visor y su rifle, y que permita que su proyectil impacte en el blanco situado a la distancia deseada.
Eso es lo que se denomina: Poner a cero un visor y realizar la tabla balística.
Es decir, hacer que lo que se observa en la posición central mirando por el visor, estando la torreta situada en el “cero”, coincida con el impacto del proyectil a una distancia conocida.
En el caso de la tabla balística que estamos usando como ejemplo, vemos que eso ocurre (en MRAD) tanto a 20 metros como a 50 metros.
Cosas de las parábolas balísticas, que tienen la costumbre de cruzarse con la recta formada por la línea de visión del visor, en dos puntos.
En cualquier otro caso deberemos mover la torreta para que al subir o bajar el número de MRAD o MOAS que nos indique nuestra aplicación balística alcancemos el objetivo a la distancia que este se encuentre.
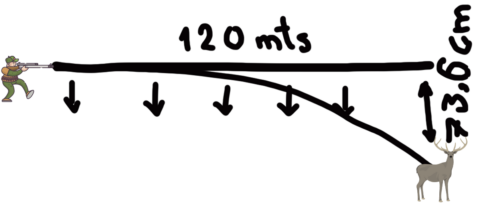
Es decir, si usaremos la tabla de nuestro ejemplo para impactar en un objetivo que se encuentre a 120 metros, que habremos medido con un telémetro o calculado con nuestro visor (como lograr eso será objeto de otro articulo en próximos números), tendremos que mover nuestra torreta 3,1 MRADS o 10,8 MOAS para elevar el punto de impacto los 73,6 cm que nuestro proyectil ya habrá “caído” a esa distancia y así lograr que impacte en el objetivo y no se entierre en el suelo.
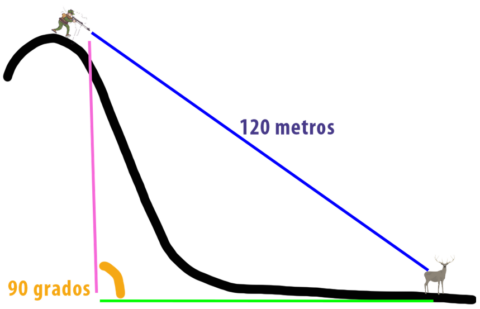
Pero ¿y si el objetivo en el que deseamos impactar no está en la misma horizontal que el tirador? Es decir, ¿y si estamos en lo alto de nuestra montaña favorita, o es el objetivo el que se encuentra sobre la misma y nosotros estamos en el llano?
¿Tendremos que apuntar por encima o por debajo del punto en el que lo haríamos si estuviera sobre la misma horizontal que el nosotros?
Recordemos que la gravedad no afecta de una forma diferente a la bala dependiendo del ángulo en el que se produzca el disparo.
La gravedad siempre es la misma, a lo largo de todo el recorrido del proyectil, sin importar en que dirección “vuelen” los proyectiles.
Pero el “ángulo” con el que la fuerza de la gravedad afectara a la trayectoria “ideal” del proyectil, ese si va a depender del que la propia trayectoria del proyectil formara respecto al eje del centro terrestre.
Intentaré explicarlo de una manera sencilla:
Como ya vimos en los gráficos anteriores, si disparamos a 120 metros directamente a nivel del suelo, la gravedad horizontal afectará a nuestro proyectil haciendo que este realice una parábola que terminará haciendo que impacte en el suelo. Separándose cada vez más de la trayectoria ideal. De hecho, a esa distancia, impactará 73,6 centímetros por debajo de esa línea ideal, o lo que es lo mismo 10,8 minutos de ángulo. Por lo que tendré que ajustar mi visor para compensar esa caída.
Cuando disparo en ángulos mayores a cero el proyectil no cae tanto, lo que me causará un verdadero problema para saber cuánto tengo que ajustar mi visor en cada momento.
Aunque hay una manera sencilla de verlo, intentaré explicarla:
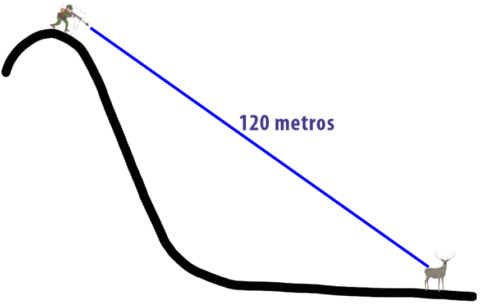
Vayamos al escenario del caso más extremo. Tenemos el objetivo directamente debajo nuestro, por lo que tenemos que realizar el disparo apuntando directamente hacia el suelo, como en el siguiente dibujo.
El acantilado vertical, es lo suficientemente alto como para que mi objetivo se encuentre a esos mismos 120 metros de la boca de mi rifle… pero totalmente en vertical y debajo de mí, por lo que la gravedad está afectando al proyectil siempre en el mismo punto. Es decir, la gravedad no va a desviar al proyectil de su trayectoria ideal en ningún momento.
Así que a 120 metros no va a existir una desviación de 73.6 centímetros de la trayectoria ideal, de hecho, no va a existir ninguna. En lo referente a la gravedad es como si el objetivo hubiera estado justo a la salida del cañón, aunque esté situado a 10 kms del mismo.
Es decir, para disparar a un objetivo totalmente perpendicular hacia abajo, no tendremos que realizar ningún ajuste en el visor, ya que es como si disparamos en la boca del cañón, y la boca del cañón está a CERO metros, CERO centímetros de distancia de ella misma.
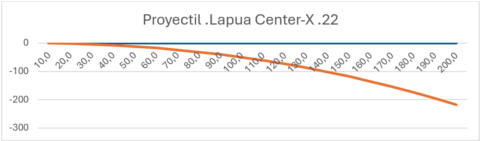
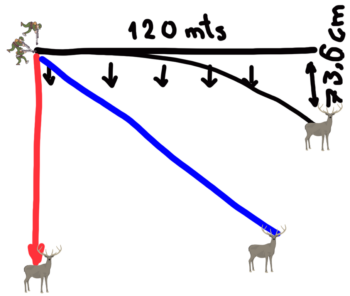
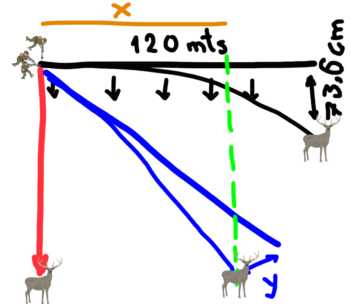
Siguiendo el mismo razonamiento, si el disparo lo realizo justo con un ángulo intermedio, entre los dos que he dibujado hasta ahora…
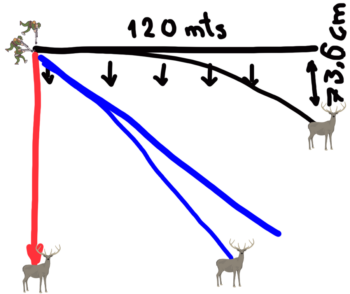
Observaremos que respecto a la trayectoria ideal que muestra el dibujo anterior, la trayectoria real se desvía más que en caso de la línea roja, pero menos que la negra.
El motivo es que ahora la gravedad está “tirando” de nuestro proyectil durante un tiempo menor que en el caso de la línea negra, y mayor que en el de la línea roja. Eso hace que realmente el proyectil cubra mucho menos terreno sobre la proyección del plano horizontal, la línea negra.
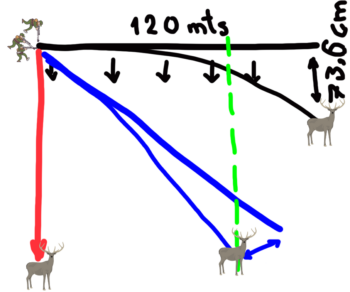
En el gráfico anterior, podemos ver que la distancia que se desvía la trayectoria real, de la ideal en el caso de la línea azul, es mucho menor que la que se desvió en la línea negra, aunque aún no sabemos cuánto es. Y también podemos ver que la línea verde que marca el final de la trayectoria real de la línea azul, cuando cruza sobre la línea negra que indicaba los 120 metros, lo hace mucho antes de llegar a esos 120 metros “horizontales al plano”. Es decir, el proyectil recorre menos de los 120 metros.
Por lo que si ajusto mi visor para que se eleve 73.6 cms, para tirar a 120 metros con un ángulo distinto a la horizontal, al tener en cuenta no solo la distancia hasta el blanco, sino también dicho ángulo… Y al ser siempre menor la “caída” o desviación de la trayectoria real respecto a la trayectoria horizontal, estaré tirando siempre por encima del punto de impacto deseado.
Entonces, ¿Cómo saber dónde debo apuntar exactamente?
El objetivo debe ser conocer la distancia real que recorrerá el proyectil sobre la horizontal, ya que es sobre esa distancia sobre la que hemos calculado nuestra tabla balística.
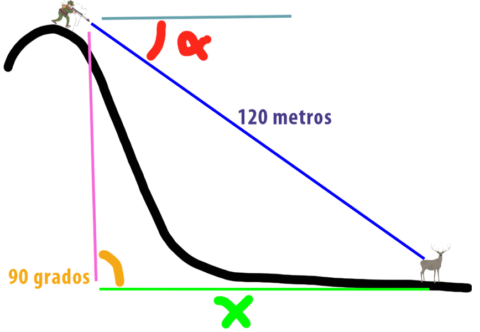
Distancia que en el gráfico anterior he dibujado en naranja, apreciando claramente que es mucho menor que los 120 metros que recorría el proyectil en el caso del disparo sobre el plano horizontal, pero que aún no sabemos cuánto mide (la llamaremos “X”), y que una vez que lo sepamos, podremos conocer cuanto debo ajustar mi torreta para que el proyectil de en el blanco a esa distancia “sobre la línea horizontal “ de tiro y que coincidirá con el ajuste a realizar sobre los 120 metros a los 45 grados que estoy realizado el disparo.
Como siguiente paso, al valor que me indica cuanto debo mover la torreta de mi visor, lo llamaremos “Y”… de momento.
Pero repasemos un poco de trigonometría de la que estudiamos en el colegio de pequeños, para poder explicar cómo calcular el valor de X.
Y pensar que llevamos toda la vida diciendo que la trigonometría no nos iba a servir para nada.
Volvamos a nuestro tirador subido en la montaña y al objetivo a 120 metros en línea recta, con un ángulo de tiro, como en el caso de la trayectoria azul del gráfico anterior, de 45º.
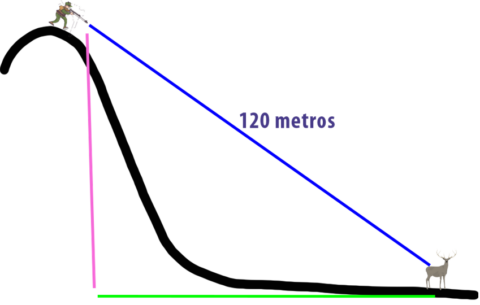
Echémosle un poco de imaginación y “veamos” un triángulo sobre esa ilustración.
La base de ese triangulo, la línea verde, es la distancia que realmente recorrerá nuestro proyectil y por lo tanto es la distancia que queremos averiguar. ¿Cómo nos ayuda la trigonometría?
Como sabemos que el ángulo entre las líneas verde y rosa siempre será de 90 grados, sabemos que el triángulo siempre será un triángulo rectángulo.
UNA DE ANGULOS
Si nos fijamos el algulo ALFA más el ángulo ALFA PRIMA, forma uno de 90 grados.
Igual que ocurre con la suma de los ángulos BETA y BETA PRIMA.
Como la línea de 120 metros, que es la diagonal que los forma, es tangente al origen de ambos pares de ángulos, esta los divide en parejas iguales pero invertidas.
Es decir ALFA es igual a BETA y ALFA PRIMA es idéntico al ángulo BETA.
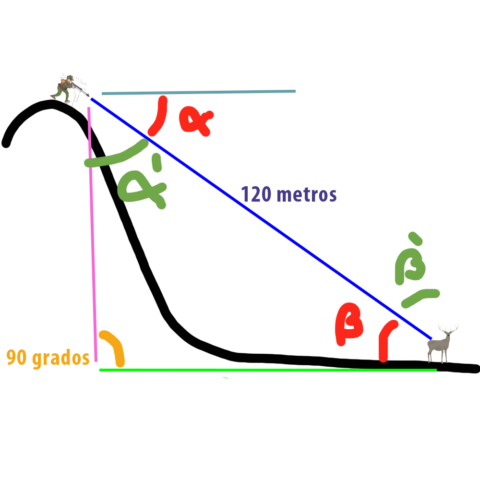
Y cómo en los triángulos rectángulos, los ángulos ALFA y BETA son exactamente iguales… conociendo el ángulo BETA y la distancia de la hipotenusa, los 120 metros, puedo calcular el tamaño del cateto verde, la que necesito saber para ajustar mi torreta…
Pues ya puedo avanzar…
ALFA hemos dicho que eran los 45 grados que me desviaba de la horizontal para realizar el disparo.
Si ya vamos intuyendo que esto afecta igual si el disparo es hacia abajo, que hacia arriba, pero vamos a dejar algo para el final.
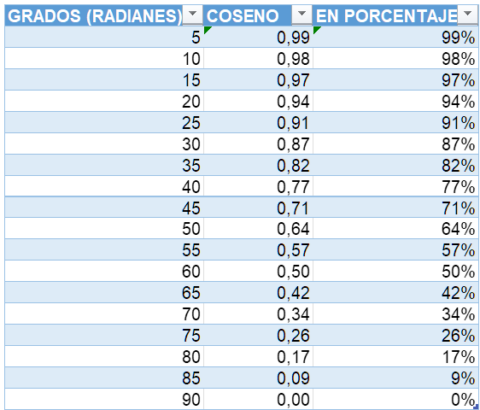
Y sabemos que la longitud de cada uno de los catetos se puede calcular multiplicando el tamaño de la hipotenusa (120 metros), por el coseno del ángulo que lo delimita, y que no es el de 90 grados, es decir: el coseno de 45 grados.
Así que tiramos de tabla de cosenos:
Y para calcular lo que mide la distancia X, en verde, buscamos el valor del coseno de 45 en nuestra tabla y lo multiplicamos por el de los 120 metros que hemos medido con nuestro telémetro.
X = 120 metros x 0.71 (coseno de 45º)
X = 85,20 metros
Nuestro tirador amigo, subido a la montaña, ya puede corregir su visor para que el disparo que haga a esa distancia sea efectivo. Solo debe utilizar su tabla balística e identificar cuanto debe mover su torreta para que el proyectil alcance el blanco.
Según la tabla que llevamos usando desde el principio de la explicación, debe subir 1,4 MRAD (media entre 1,2 y 1,6 que indica para 80 y 90 metros) o 4.8 MOAS (media entre 4,0 y 5,6 que indica para 80 y 90 metros), para recuperar la caída del proyectil, los 40 cm que habrá bajado respecto a la trayectoria ideal (media entre 31,6 y 40,3 que indica para 80 y 90 metros).
Por lo tanto, tendrá que apuntar 40 cm por debajo del cero de su visor, no los 73.6 cm que tendría que haberlo hecho si hubiera tirado en horizontal. Y como la trigonometría en el caso que nos ocupa no distingue si el triángulo rectángulo está boca arriba, boca abajo o de lado… sino que se basa siempre en la posición de los catetos respecto al ángulo de 90 grados… da igual que disparemos hacia arriba, que lo hagamos hacia abajo, el disparo siempre, siempre, deberemos hacerlo más bajo de lo que lo haríamos sobre la horizontal.
La buena noticia, para compensar esto de los cosenos y las hipotenusas, es que en la naturaleza raramente nos encontraremos con un grado mayor de 30 grados, salvo que estemos mirando un precipicio como el del ejemplo.
Y como en el mercado tenemos una gran variedad de inclinómetros, tanto electrónicos, como mecánicos (que incluso nos facilitan el valor del coseno directamente), como aplicaciones para el móvil, o que se pueden acoplar a nuestros rifles, con un poco de práctica podremos dejar de fallar esos disparos por estar por encima o por debajo nuestro estábamos perdiendo hasta ahora.
Hoy en día también existe tecnología electrónica que nos facilita este trabajo, cualquier telémetro de calidad, ya sea monocular o binocular, es capaz de medir el ángulo del disparo que queremos efectuar y calcular la distancia real (hipotenusa) al que se encuentra nuestro blanco.
Una vez conocidos esos datos, el aparato nos indica en la pantalla; o bien ambos datos para que nosotros realicemos el cálculo, o bien lo realiza el dispositivo y nos muestra la medida CORREGIDA, ósea la medida real que deberíamos utilizar en nuestro programa balístico para disparar.